BIENVENIDOS

ÁREA DE  MATEMÁTICA

Señores Padres  de  Familia y Estudiantes en este blogg encontrarán los temas correspondientes al Parcial 4 en el área de Matemática y las tareas que deberán realizar los estudiantes.

UNIDAD 4

TU PROBLEMA  ES MI PROBLEMA


      FRACCIONES SIMPLES,  REPRESENTACIÓN GRÁFICA

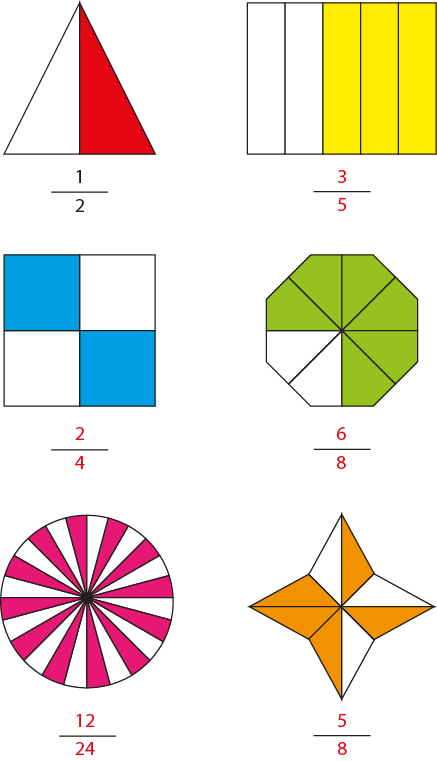
Una fracción  se representa por dos números separados por una línea horizontal.  Para  la representación gráfica se usa cualquier figura geométrica. El área pintada representa el numerador y las partes en las que se divide la figura representan el denominador.

AMPLIFICACIÓN Y SIMPLIFICACIÓN DE FRACCIONES

Amplificar Fracciones

Significa  multiplicar el denominador y numerador de una fracción por un mismo número . Esta acción permite que tanto el denominador como el numerador de la fracción aumenten de valor tantas veces como veces se amplifica, pero el valor de la fracción como tal, se mantiene igual.

Ejemplos:

Fracciones amplificadas por  x 3.

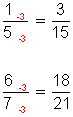
Simplificar  Fracciones

Significa dividir por un mismo número tanto el numerador como el denominador, para que la fracción (mostrada ahora con números distintos pero menores) mantenga su proporcionalidad  (que su valor se mantenga).

Sólo se podrán simplificar fracciones cuando el  numerador y denominador sean divisibles por un número común.

Cada vez que se simplifique una fracción se debe llegar hasta la fracción irreductible , es decir, aquella fracción que no se puede simplificar más.

Ejemplos:

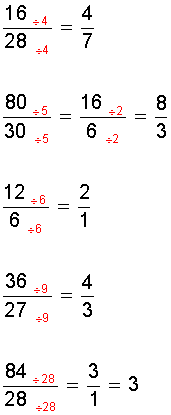
VIDEO

TAREA DE MATEMÁTICA 

DESCARGAR TAREA DE MATEMÁTICA  DAR CLICK



Martes, 24 de Marzo del 2020

Fracciones Simples en la semirrecta numérica

Cuando todas las fracciones tienen el mismo denominador, las fracciones con menor numerador se ubican a la izquierda y los que tienen mayor numerador a la derecha. Es decir se debe tomar en cuenta al numerador para ubicar en la semirrecta.

Ejemplos:

1.- Observe la siguiente semirrecta y la ubicación de las fracciones.

2.- Cuando tenemos fracciones que podemos simplificar  que significa dividir al numerador y al denominador para el mismo número lo hacemos de la siguiente manera.

- A la fracción 2/8 podemos simplificar a la mitad o dividir para 2 tanto al numerador como al denominador quedando 1/4.

- A la fracción 4/8 podemos simplificar a la mitad o dividir para 2 tanto al numerador como al denominador quedando 2/4.

- A la fracción 6/8 podemos simplificar a la mitad o dividir para 2 tanto al numerador como al denominador quedando 3/4.

- A la fracción 8/8 podemos simplificar o sacar la octava  parte que significa dividir para 8 tanto al numerador como al denominador quedando 1.

Otros Ejemplos:

Video

Relación de Orden entre Fracciones

Los símbolos que se utilizan para hacer comparaciones entre fracciones son: “mayor que” (>) “menor que” (<),  "igual que" (=).

Los signos “mayor que”  y “menor que” se parecen a la letra “v” girada.  Podemos ayudarnos de este truco para saber hacia qué lado debe estar:

La apertura grande siempre señala al elemento más grande, y la terminación más pequeña, la punta, al más pequeño. De esta manera es más fácil recordarlo.

La primera persona en usar este signo = fue el médico y matemático Robert Recorde, quien explicó que no hay dos cosas que puedan ser más iguales que dos líneas paralelas. Por eso empezó a usar este símbolo para representar la igualdad.

Se utiliza para expresar elementos que son iguales y se lee “igual que”.

Procesos para determinar la relación de orden entre dos fracciones
Método Multiplicación Cruzada

Ejemplos:

Video

Procesos para determinar la relación de orden entre tres fracciones

Ejemplo:

1.- Observar las fracciones, ordenar de menor a mayor.

2.- Debemos amplificar que significa multiplicar para que todos los denominadores tengan el número 20.
3.- A la fracción 2/5 debemos multiplicar X 4 al numerador y al denominador.
4.- A la fracción 1/10 debemos multiplicar x 2 al numerador y al denominador
5.- A la fracción 3/20 no multiplicamos porque ya tiene 20 en el denominador.

6.- Las fracciones de menor a mayor son:

Tarea en el cuaderno

DESCARGAR TAREA AQUÍ

Martes, 31 de marzo del 2020

Perímetro de Figuras Geométricas

El perímetro de toda figura geométrica se obtiene sumando la longitud de sus lados.
Para calcular el perímetro se usa la siguiente fórmula:

P= Perímetro
L= Lado

P= L+L+L+L  
(Depende de cuántos lados tiene la figura geométrica)

Perímetro de Paralelogramos y Trapecios

Para calcular el perímetro de cualquier paralelogramo o trapecio usamos la fórmula:

P= L+L+L+L       

Porque todos los paralelogramos y trapecios tienen 4 lados.

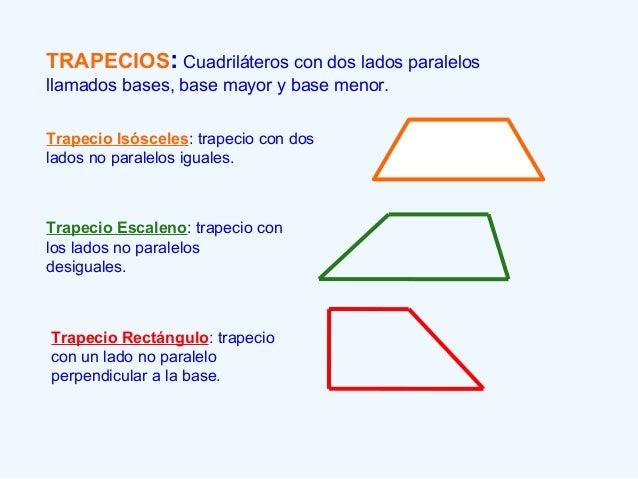
Ejemplos:

Cuadrado



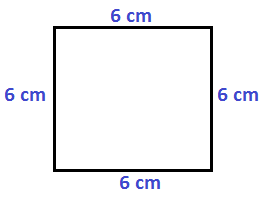
P=  L + L + L + L
P=  6 + 6 + 6 + 6 
P= 24 cm

Romboide




P=  L + L + L + L
P=  8 + 4 + 8 + 4 
P= 24 cm



Trapecio Isósceles



P=  L + L + L + L
P=  7 + 8 + 10 + 8
P=  33 cm

Perímetro  de  Triángulos

Para calcular el perímetro de cualquier triángulo se usa la siguiente fórmula:

P= L + L+ L       

Porque cualquier triángulo tiene tres lados.


Ejemplos:

Triángulo Escaleno


P= L + L+ L
P= 2 + 5 + 4
P= 11 cm

Triángulo Isósceles

P= L + L + L
P= 6 + 8 + 6
P= 20 cm

Triángulo Equilátero



P= L + L + L
P= 2 + 2 + 2
P= 6 cm

Video

Tarea 

Para descargar Tarea dar click

Martes 7 de abril del 2020

Diagrama de Barras

Ejemplos:

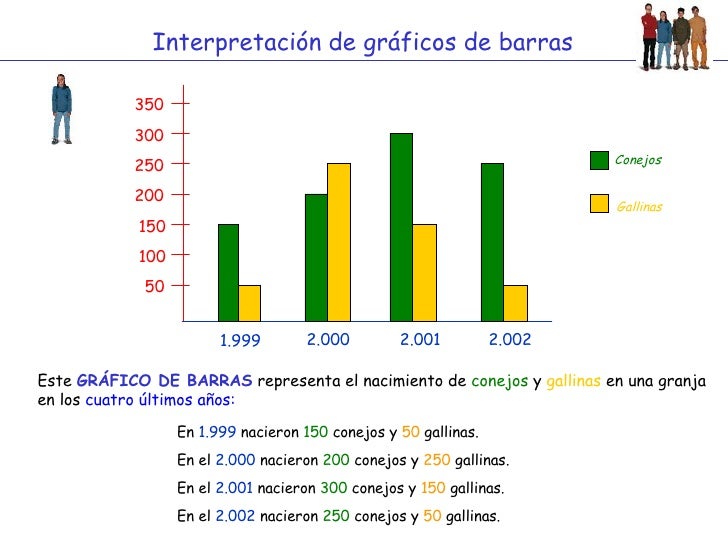
EJERCICIOS PARA PRACTICAR

CONTESTE DE FORMA ORAL LAS PREGUNTAS DE LOS EJEMPLOS

• ¿Qué película es la preferida?
• ¿Cuántas personas prefieren la película de Los Pitufos?

• ¿Cuáles son los deportes que practican igual cantidad de personas?
• ¿Cuántas personas practican atletismo?

• ¿Cuál es la comida menos preferida?
• ¿Cuál es la comida preferida de los niños?

Video

Para prácticar ejercicios de diagrama de barras dar click 

Tarea 
Cuaderno de trabajo páginas 35 y 36

Martes 14 de Abril del 2020

Patrones Numéricos Decrecientes

Un patrón numérico se establece restando o dividiendo el primer término por un número constante, a fin de obtener el segundo término y así sucesivamente.

Patrones Decrecientes con Resta







Patrones Decrecientes con División


Problema Matemático

Mateo tiene 810 cromos para llenar el álbum. Si el primer día pega la tercera parte de sus cromos, al siguiente día coloca la tercera parte de lo que pegó el día anterior y así sucesivamente:

¿En qué día pega diez cromos?

Videos

Patrón Númerico Decreciente

Patrones Decrecientes

Deber en el cuaderno

Para descargar el deber dar click

Martes 21 de Abril del 2020

Números Decimales

Un número decimal tiene:
- Parte Entera
- Coma
- Parte Decimal

La coma sirve para separar la parte entera de la parte decimal.

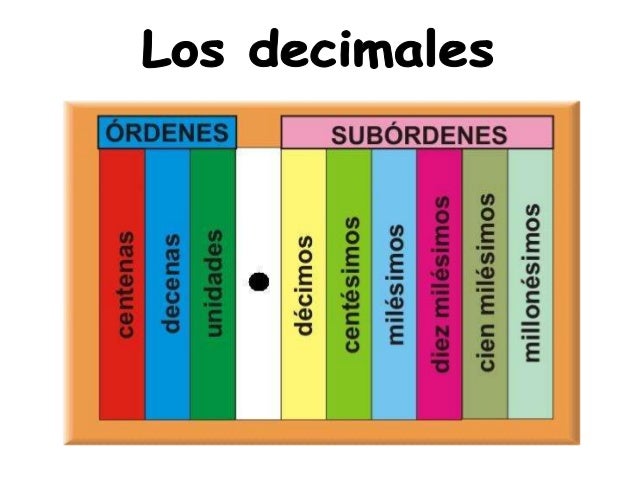
Ejemplos:

Ubicar en la tabla posicional los siguientes ejemplos:

Lectura de las cantidades de la tabla:

a) Cero enteros doce centésimos

b) Veinte y cinco enteros cuarenta y cinco centésimos

c) Diecisiete enteros seiscientos cinco milésimos

d) Ciento setenta y ocho enteros cinco centésimos

Videos

¿Qué son los Números Decimales?

Cómo leer Números Decimales

Tarea en el cuadernillo de trabajo páginas 49 y 50.

Martes, 28 de Abril del 2020

Números Decimales

 Ejemplos:

Se Lee:  Trescientos cuarenta y cinco enteros con seiscientos veinte y cuatro milésimas.

Trescientos cuarenta y cinco coma con seiscientos veinte y cinco milésimas.

Transformar de un número Fraccionario a número Decimal

Ejemplos:

Vídeos

Cómo pasar de Fracción decimal a Número decimal

Convertir Fracción en Decimal

Deber 

Para descargar el deber dar clic aquí

Martes, 5 de Mayo del 2020

Números Decimales a Fraccionarios

Ejemplos:

Vídeo

Convertir decimal a Fracción

Deber

Resolver las actividades del cuaderno de trabajo.

Martes, 12 de Mayo del 2020

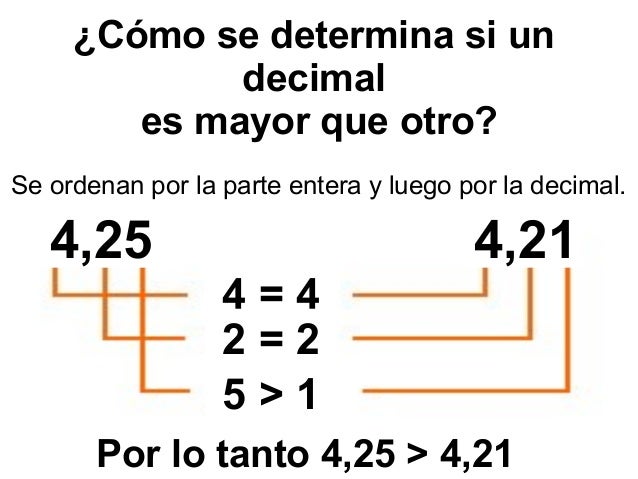
Relación de orden entre decimales

Para comparar números decimales hay que tener en cuenta lo siguiente:

Ejemplos:

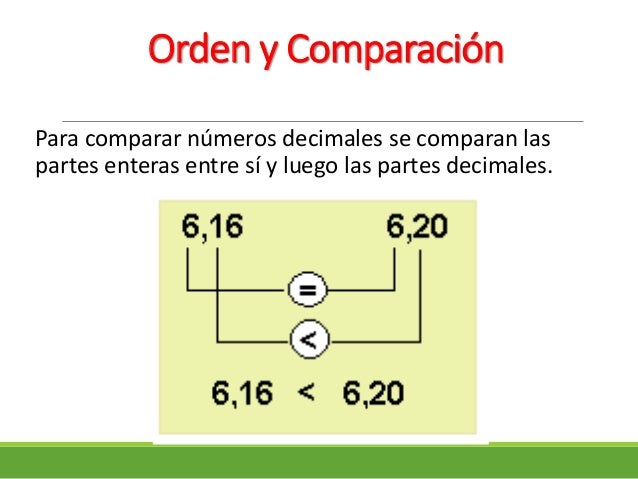
Video

Orden de los Números Decimales

Deber:

Realizar la hoja de trabajo

Para descargar el deber dar click aquí.

Martes, 19 de Mayo del 2020

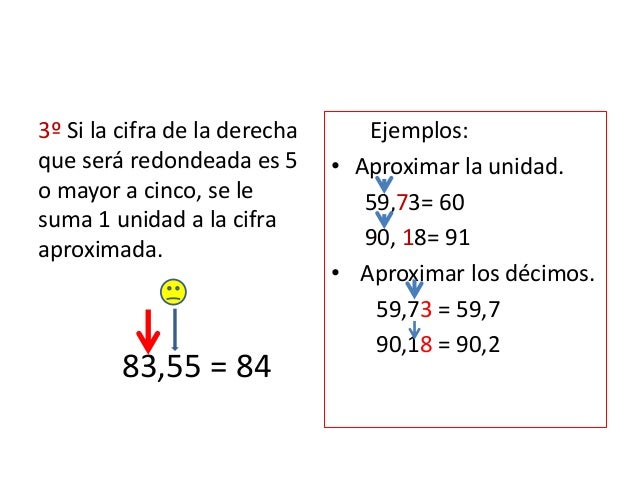
Redondear Números Decimales

Vídeo

Redondeo de Números Decimales

Deber:

Realizar las actividades de la página 60 del cuadernillo

Martes, 26 de Mayo del 2020

Adiciones, Sustracciones y Multiplicaciones con Números Decimales.

Ejemplos:

Sumas

Restas

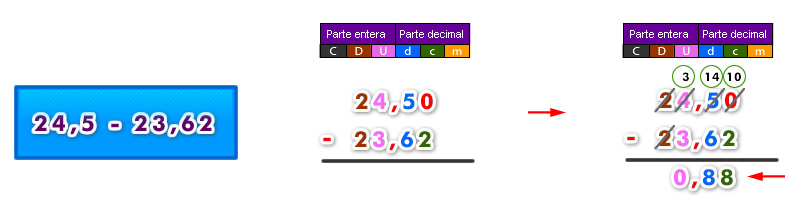
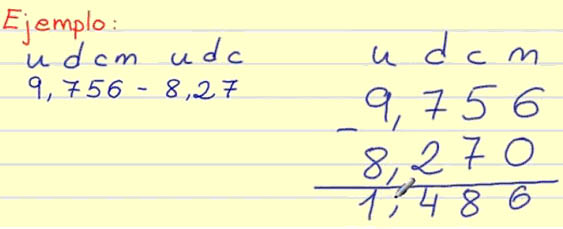
Multiplicaciones

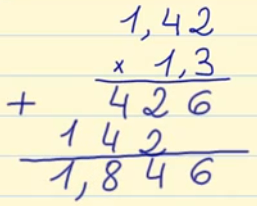
Vídeo

Suma y resta con números decimales

Multiplicación con números decimales

Deber

Resolver la hoja de trabajo sobre sumas, restas y multiplicaciones con números decimales.

Martes, 2 de junio del 2020

Proporcionalidad Directa

La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa. Para hacer una regla de tres simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud.

Ejemplos:

Vídeo

Regla de tres simple directa

Deber

Realizar las actividades del cuadernillo página 78.

Martes, 9 de junio del 2020

Metro Cuadrado, Metro Cúbico y Medidas de Masa

Metro Cuadrado

Metro Cúbico

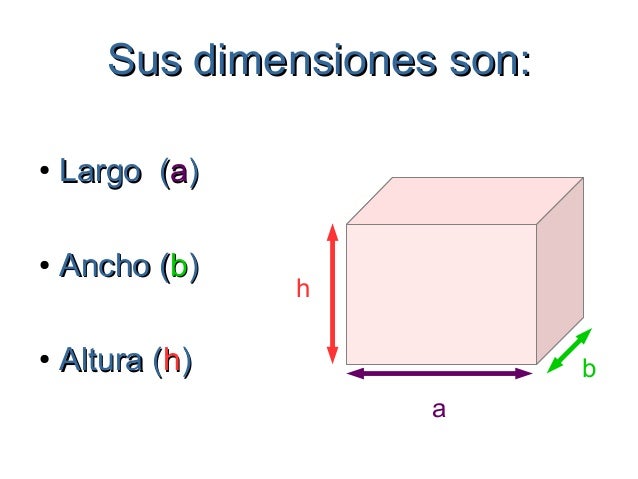
Ejemplo:

Medidas de masa

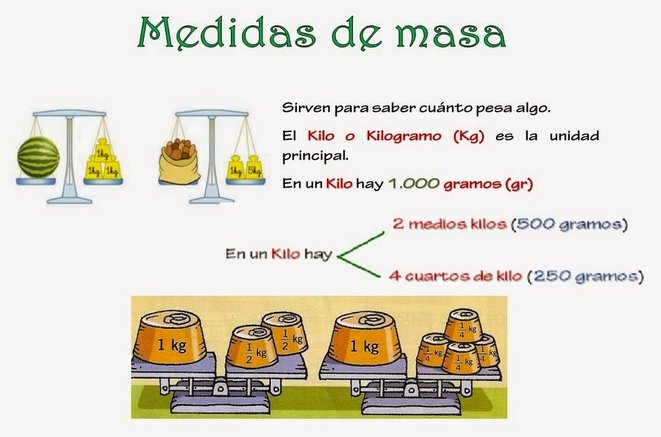
Vídeos:

Medidas de Superficie

Medidas de Volumen

Medidas de Masa

Deber

Realizar la hoja de trabajo en el cuaderno.

Para descargar el deber dar clic aquí

Martes, 16 de Junio del 2020

Vídeo

Cómo calcular el rango

Deber

Realizar las actividades del cuadernillo página 83.